报告题目:从收缩算法的统一框架到广义的PPA算法
报告人:何炳生 教授(南京大学)
主持人:王祥丰 副教授
报告时间:2024年1月15日(星期一)14:15-15:15
报告地点:华东师范大学普陀校区教书院105
报告摘要:
线性约束的凸优化问题对拉格朗日函数的鞍点,跟结构型单调变分不等式
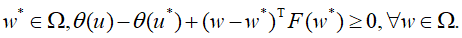
的解集是等价的。变量为![]() 的经典的临近点算法(PPA),其迭代序列
的经典的临近点算法(PPA),其迭代序列![]() 具有
具有
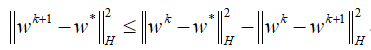
和
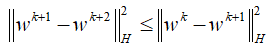
这样非常漂亮的性质,其中![]() 为正定矩阵。
为正定矩阵。
乘子交替方向法(ADMM)中,每次迭代从给定的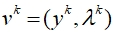 开始,给出新的
开始,给出新的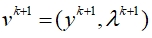 。ADMM的核心变量的迭代序列
。ADMM的核心变量的迭代序列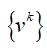 同样具有
同样具有
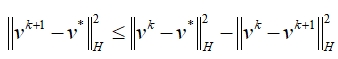
和
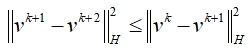
这样的性质,这些性质也为一些加速ADMM方法提供了支撑。
我们对一般的凸优化问题所对应的变分不等式,通过Gauss型预测-校正,构造了相应的容易实现的广义临近点算法(Generalized PPA),其迭代产生的序列同样具有上面所述的漂亮性质,为拓展凸优化算法设计提供了新的思路。
报告人简介:
何炳生,南京大学数学系77级本科毕业后公派去联邦德国留学,师从巴伐利亚科学院院士Stoer, 取得维尔茨堡大学博士学位后于1987年开始在南京大学数学系工作,1997年晋升为教授。在职期间,曾获江苏省科技进步一等奖,获评江苏省有突出贡献的中青年专家。退休后,2014年获《中国运筹学会科学技术奖》运筹研究奖,2016年获首届《江苏省工业与应用数学》突出贡献奖,2018年获《高等学校科学研究优秀成果奖》自然科学二等奖。
长期从事最优化理论与方法的研究,在投影收缩算法和以ADMM为代表的分裂收缩算法优化领域做出了一批有特色的工作,提出了一个简单的能用来指导设计构造凸优化分裂收缩算法的统一框架。部分成果被包括美国科学院院士、工程院院士和连续四届《世界数学家大会》大会邀请报告人在内的国际著名学者大篇幅引用。代表性算法被用来有效地解决了一些(其他方法在规模或速度上满足不了计算要求的)工程计算问题。

